Introducción al Calculo diferencial .
En cálculo diferencial y análisis
matemático, la derivada de una función es la razón de cambio instantánea con la
que varía el valor de dicha función matemática, según se modifique el valor de
su variable independiente. La derivada de una función es un concepto local, es
decir, se calcula como el límite de la rapidez de cambio media de la función en
cierto intervalo, cuando el intervalo considerado para la variable
independiente se torna cada vez más pequeño. Por eso se habla del valor de la
derivada de una función en un punto dado.
Un ejemplo habitual aparece al
estudiar el movimiento: si una función representa la posición de un objeto con
respecto al tiempo, su derivada es la velocidad de dicho objeto para todos los
momentos. Un avión que realice un vuelo transatlántico de 4500 km entre las 12:00
y las 18:00, viaja a una velocidad media de 750 km/h. Sin embargo, puede estar
viajando a velocidades mayores o menores en distintos tramos de la ruta. En
particular, si entre las 15:00 y las 15:30 recorre 400 km, su velocidad media
en ese tramo es de 800 km/h. Para conocer su velocidad instantánea a las 15:20,
por ejemplo, es necesario calcular la velocidad media en intervalos de tiempo
cada vez menores alrededor de esta hora: entre las 15:15 y las 15:25, entre las
15:19 y las 15:21.
Entonces el valor de la derivada
de una función en un punto puede interpretarse geométricamente, ya que se
corresponde con la pendiente de la recta tangente a la gráfica de la función en
dicho punto. La recta tangente es, a su vez, la gráfica de la mejor
aproximación lineal de la función alrededor de dicho punto. La noción de
derivada puede generalizarse para el caso de funciones de más de una variable
con la derivada parcial y el diferencial.
Historia de la derivada
Los problemas típicos que dieron
origen al cálculo infinitesimal comenzaron a plantearse en la época clásica de
la antigua Grecia (siglo III a. C.), pero no se encontraron métodos
sistemáticos de resolución hasta diecinueve siglos después (en el siglo XVII
por obra de Isaac Newton y Gottfried Leibniz).
En lo que atañe a las derivadas existen
dos conceptos de tipo geométrico que le dieron origen:
El problema de la tangente a una
curva (Apolonio de Perge)
El Teorema de los extremos:
máximos y mínimos (Pierre de Fermat)
En su conjunto dieron origen a lo
que actualmente se conoce como cálculo diferencial.
Los matemáticos perdieron el
miedo que los griegos les habían tenido a los infinitesimales: Johannes Kepler
y Bonaventura Cavalieri fueron los primeros en usarlos, empezaron a andar un
camino que llevaría en medio siglo al descubrimiento del cálculo infinitesimal.
A mediados del siglo XVII las
cantidades infinitesimales fueron cada vez más usadas para resolver problemas
de cálculos de tangentes, áreas, volúmenes; los primeros darían origen al
cálculo diferencial, los otros al integral.
A finales del siglo XVII se
sintetizaron en dos conceptos los algoritmos usados por sus predecesores, en lo
que hoy llamamos «derivada» e «integral». La historia de la matemática reconoce
que Isaac Newton y Gottfried Leibniz son los creadores del cálculo diferencial
e integral. Ellos desarrollaron reglas para manipular las derivadas (reglas de
derivación) e Isaac Barrow demostró que la derivación y la integración son
operaciones inversas.
Newton desarrolló en Cambridge su
propio método para el cálculo de tangentes. En 1665 encontró un algoritmo para
derivar funciones algebraicas que coincidía con el descubierto por Fermat. A
finales de 1665 se dedicó a reestructurar las bases de su cálculo, intentando
desligarse de los infinitesimales, e introdujo el concepto de fluxión, que para
él era la velocidad con la que una variable «fluye» (varía) con el tiempo.
Gottfried Leibniz, por su parte,
formuló y desarrolló el cálculo diferencial en 1675. Fue el primero en publicar
los mismos resultados que Isaac Newton descubriera 10 años antes, de manera
independiente. En su investigación conservó un carácter geométrico y trató a la
derivada como un cociente incremental y no como una velocidad, viendo el sentido
de su correspondencia con la pendiente de la recta tangente a la curva en dicho
punto.
Leibniz es el inventor de
diversos símbolos matemáticos. A él se deben los nombres de: cálculo
diferencial y cálculo integral, así como los símbolos de derivada dy/dx.
La derivada.
En terminología clásica, la
diferenciación manifiesta el coeficiente en que una cantidad y cambia a consecuencia de un cambio en otra
cantidad x.
En matemáticas, coeficiente es un
factor multiplicativo que pertenece a cierto objeto como una variable, un
vector unitario, una función base, etc.
En física, coeficiente es una
expresión numérica que mediante alguna fórmula determina las características o
propiedades de un cuerpo.
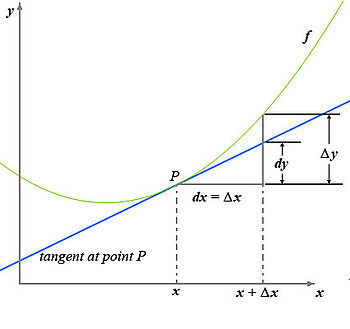
En nuestro caso, observando la
gráfica de la derecha, el coeficiente del que hablamos vendría representado en
el punto P de la función por el resultado de la división representada por la
relación d y dx que como puede
comprobarse en la gráfica, es un valor que se mantiene constante a lo largo de
la línea recta azul que representa la tangente en el punto P , de la función.
Esto es fácil de entender puesto que el triángulo rectángulo formado en la
gráfica con vértice en el punto P por mucho que lo dibujemos más grande, al ser
una figura proporcional el resultado de d y/ d x siempre el mismo.
Esta noción constituye la
aproximación más veloz a la derivada, puesto que el acercamiento a la pendiente
de la recta tangente es tanto por la derecha como por la izquierda de manera
simultánea
Aplicaciones de la derivada
Métodos para obtener la derivada de una función.
Si bien se ha entendido la derivada de una función como la tasa instantánea de cambio en una función, los métodos de obtención de derivadas usan esta definición como base para obtención de formulas directas para su obtención.
Un primer método, y del cual se obtienen generalidades para la definición de formulas de derivadas es la Regla de los cuatro pasos,
Como se puede observar el método de los cuatro pasos resulta en un proceso laborioso de obtener la derivada de una función. Por lo que no se considera lo mas adecuado para obtener la derivada de funciones, su importancia radica que aplica la definición de derivada y permite la obtención de formulas que son aplicables a todo tipo de funciones y cuya resolución es más rápida y práctica.
Formulas de derivación
Las formulas de derivación se clasifican de acuerdo al tipo de funciones:
1. Formulas algebraicas: que permiten obtener derivadas de funciones que se expresan mediante reglas algebraicas básicas. Como son: función constante, función identidad, función polinomio, función de potencias constantes, función que presentan productos y funciones que se están dividiendo
2. Formulas para funciones trascendentes: que se clasifican en:
a) Funciones exponenciales y logarítmicas:
b) Funciones trigonométricas
c) Trigonométricas inversas: donde U' es la derivada de la función
Uso de las formulas de derivación .
El uso de las formulas de derivación implica el reemplazo de los valores variables en las funciones y para lograrlo de manera eficiente es importante adquirir mecanismos de solución mediante la practica constante de ejercicios de cada tipo de función.
Es conveniente iniciar con ejercicios básicos de derivadas de funciones algebraicas haciendo énfasis en la importancia de la denotación de la primera derivada usando el método de Lagrange y reemplazando adecuadamente cada elemento de la formula.
Ejercicios básicos:



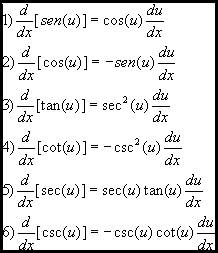

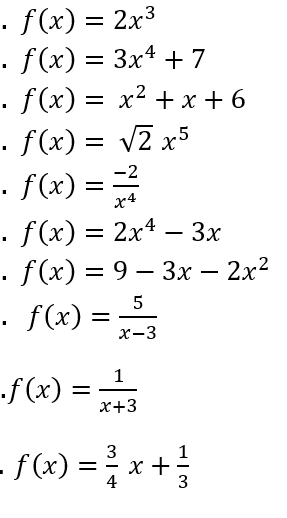
Comentarios
Publicar un comentario