MATEMATICAS II, NOS PRESENTA UNA HERRAMIENTAS MAS PARA EL DESEMPEÑO DE TODO INGENIERO: EL CALCULO DIFERENCIAL.
SI BIEN REPRESENTA UN RETO PARA LA MAYORIA DE NOSOTROS, SON DE GRAN UTILIDAD EN LA SOLUCION DE UNA GRAN CANTIDAD DE PROBLEMAS DE OPTIMIZACION DE RECURSOS EN LA INDUSTRIA.

Si bien el concepto de variación nos es familiar a todos en nuestra experiencia cotidiana, su reflexión matemática suele ser explicada de mejor manera teniendo como auxiliar: las ramas del algebra y la geometría analítica, que nos permiten entender la manera como se establece una relación de dependencia entre dos o mas variables y mas aun, como realizar un análisis de tendencias de las mismas y verificar sus tasas de cambio, es decir sus diferencias, para establecer un concepto mas a tono con el análisis diferencial: la tasa instantánea de cambio o derivada.
Para lograr este objetivo iniciaremos con la aceptación de conceptos comunes en el lenguaje del calculo diferencial:
1. Función: es una relación de dependencia entre dos variables, se representa como y=f(x)… y se lee y igual a f de x
2. Variable independiente: esta representada por "x" y se encuentra generalmente en el segundo miembro de la función, donde se establece la regla de dependencia para la variable independiente
3. Variable dependiente: esta representada por "y", se encuentra en el primer miembro de la ecuación y sus valores dependen de los valores que tome x.
4. Dominio: se define dominio al conjunto de valores que puede tomar la variable independiente, de modo tal que permita tomar valores a la variable dependiente.
5. Contradominio: se define como el conjunto de valores que puede tomar la variable dependiente y, a través de las variaciones de x.
De acuerdo a lo anterior tenemos que las funciones se pueden clasificar de diversas maneras, pero principalmente de acuerdo a la regla matemática que estas presenten: aso tenemos que las funciones pueden ser algebraicas o trascendentales, Implícitas o explicitas.
Ejemplos:
1. Ejemplo de función constante:

2. Ejemplo de función lineal:
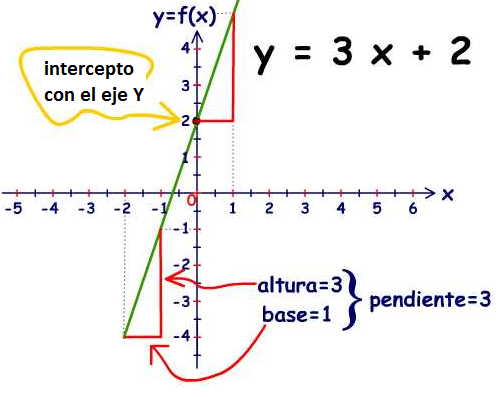
3. Ejemplo de función cuadrática:

4. Ejemplo de función logarítmica

5. Ejemplo de función exponencial:

6. Ejemplo de función trigonométrica
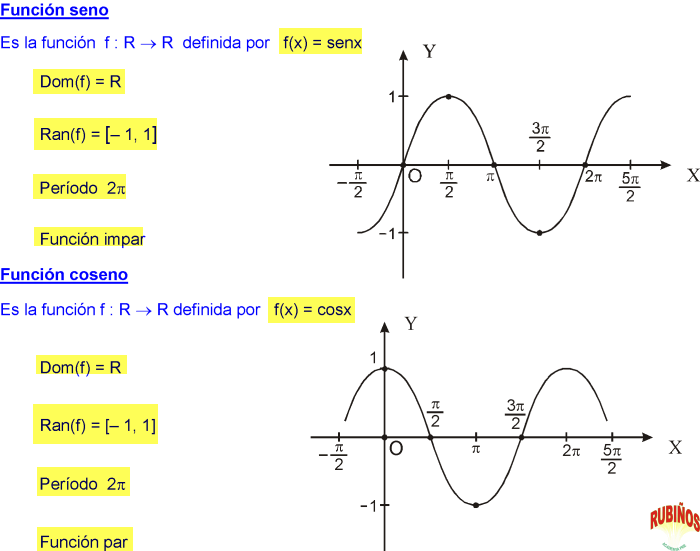
7. Ejemplo de función trigonométrica inversa

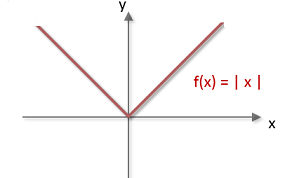
8. Ejemplo de función valor absoluto
9. Ejemplo de función escalonada

Como puedes observar existen tantos tipos de funciones como reglas matemáticas pueden darse
El concepto de función esta estrechamente ligado a su interpretación geométrica, y tiene diferencias sustanciales con el concepto de relación matemática,
Actividad 1: Completa el siguiente cuadro comparativo
SI BIEN REPRESENTA UN RETO PARA LA MAYORIA DE NOSOTROS, SON DE GRAN UTILIDAD EN LA SOLUCION DE UNA GRAN CANTIDAD DE PROBLEMAS DE OPTIMIZACION DE RECURSOS EN LA INDUSTRIA.
El calculo diferencial es una parte del análisis matemático que consiste en el estudio de como cambian las funciones cuando sus variables cambian. Esta relación de cambio entre sus variables se conoce como derivada. Y este cambio esta estrechamente relacionado con el tema de diferencia.
Así, en el concepto de derivada resalta un concepto importante, muy en especial en la ingeniería industrial: Variables.
La ingeniería industrial nos capacita para entender la interacción entre las diferentes variables que están presentes en cualquier proceso productivo o administrativo y es precisamente que el calculo diferencial nos presenta esta relación entre variables y funciones.
De acuerdo con el libro de Matemáticas para las Ciencias Sociales y Administración de Bennet, el calculo diferencial tiene varios campos de aplicación para el ingeniero industrial como son: producción, negocios y economía.

Si bien el concepto de variación nos es familiar a todos en nuestra experiencia cotidiana, su reflexión matemática suele ser explicada de mejor manera teniendo como auxiliar: las ramas del algebra y la geometría analítica, que nos permiten entender la manera como se establece una relación de dependencia entre dos o mas variables y mas aun, como realizar un análisis de tendencias de las mismas y verificar sus tasas de cambio, es decir sus diferencias, para establecer un concepto mas a tono con el análisis diferencial: la tasa instantánea de cambio o derivada.
Para lograr este objetivo iniciaremos con la aceptación de conceptos comunes en el lenguaje del calculo diferencial:
1. Función: es una relación de dependencia entre dos variables, se representa como y=f(x)… y se lee y igual a f de x
2. Variable independiente: esta representada por "x" y se encuentra generalmente en el segundo miembro de la función, donde se establece la regla de dependencia para la variable independiente
3. Variable dependiente: esta representada por "y", se encuentra en el primer miembro de la ecuación y sus valores dependen de los valores que tome x.
4. Dominio: se define dominio al conjunto de valores que puede tomar la variable independiente, de modo tal que permita tomar valores a la variable dependiente.
5. Contradominio: se define como el conjunto de valores que puede tomar la variable dependiente y, a través de las variaciones de x.
De acuerdo a lo anterior tenemos que las funciones se pueden clasificar de diversas maneras, pero principalmente de acuerdo a la regla matemática que estas presenten: aso tenemos que las funciones pueden ser algebraicas o trascendentales, Implícitas o explicitas.
Ejemplos:
1. Ejemplo de función constante:

2. Ejemplo de función lineal:

3. Ejemplo de función cuadrática:

4. Ejemplo de función logarítmica
5. Ejemplo de función exponencial:

6. Ejemplo de función trigonométrica

7. Ejemplo de función trigonométrica inversa

8. Ejemplo de función valor absoluto

9. Ejemplo de función escalonada
Como puedes observar existen tantos tipos de funciones como reglas matemáticas pueden darse
El concepto de función esta estrechamente ligado a su interpretación geométrica, y tiene diferencias sustanciales con el concepto de relación matemática,
Actividad 1: Completa el siguiente cuadro comparativo
Función Matemática
|
Relación Matemática
|

Miguel Ángel Nájera Méndez
ResponderBorrarNos servirá para calcular las variables y las derivadas.
El cálculo diferencial en la ingeniería es muy fundamental ya qué con ello podemos dedicar costos el cálculo es muy importante hoy en día.
ResponderBorrarImportancia del cálculo diferencial influye en el desarrollo en mi carrera como ing. Industrial
ResponderBorrarSoy José Alberto f. El calculo nos ayuda a una mejor optimizacion de recursos y administración
ResponderBorrarEl calculo diferencial es fundamental para ver el desarollo y recursos , que se pueden medir y calcular en un desarollo en la carrera
ResponderBorrarBryan Misael Juarez Cortes
ResponderBorrarkaren ivett dominguez monroy
me ayudara a desempeñarme a solucionar problemas cotidianos como administrativo o cosas general de la empresa