Unidad 1. Limites

1.1 Definición y generalidades.

 

El vocablo que nos ocupa en primer lugar, límite, podemos decir que se trata de una palabra que procede, etimológicamente hablando, del latín. En concreto, emana del sustantivo “limes”, que puede traducirse como “frontera o borde”.

La noción de límite tiene múltiples acepciones. Puede tratarse de una línea que separa dos territorios, de un extremo a que llega un determinado tiempo o de una restricción o limitación. Para la matemática, un límite es una magnitud fija a la que se aproximan cada vez más los términos de una secuencia infinita de magnitudes

La expresión límite de una función se utiliza en el cálculo diferencial matemático y refiere a la cercanía entre un valor y un punto. Por ejemplo: si una función f tiene un límite X en un punto t, quiere decir que el valor de f puede ser todo lo cercano a X que se desee, con puntos suficientemente cercanos a t, pero distintos

 

Dentro de lo que sería el límite de la función, tendríamos que destacar la existencia de una teoría muy importante. Nos estamos refiriendo a la teoría del sándwich, también conocida como teorema del emparedado, que tiene su origen en tiempos del físico griego Arquímedes, que la usó al igual que hiciera el matemático Eudoxo de Cnido, que era discípulo del filósofo Platón.

No obstante, se considera que el verdadero formulador de aquella no es otro que el matemático y astrónomo alemán Carl Friedrich Gauss (1777 – 1855), que ha pasado a la Historia por el calificativo de “príncipe de las Matemáticas”. Ese teorema tenemos que decir que lo que viene a establecer es que si dos funciones se decantan por el mismo límite en lo que se refiere a un punto concreto, cualquier otra función que se establezca entre ambas también compartirá con ellas el mismo límite.

Los límites de las funciones ya se analizaban en el siglo XVII, aunque la notación moderna surgió en el siglo XVIII a partir del trabajo de diversos especialistas. Se dice que Karl Weierstrass fue el primer matemático en proponer una técnica precisa, entre 1850 y 1860.

En definitiva, una función f con límite X en t quiere decir que dicha función tiende hacia su límite X cerca de t, con f(x) tan cerca de X como sea posible pero haciendo que x sea distinto de t. De todas maneras, la idea de cercanía es poco precisa, por lo que una definición formal requiere de más elementos

 

 

 1.2 Propiedades de los límites 
 

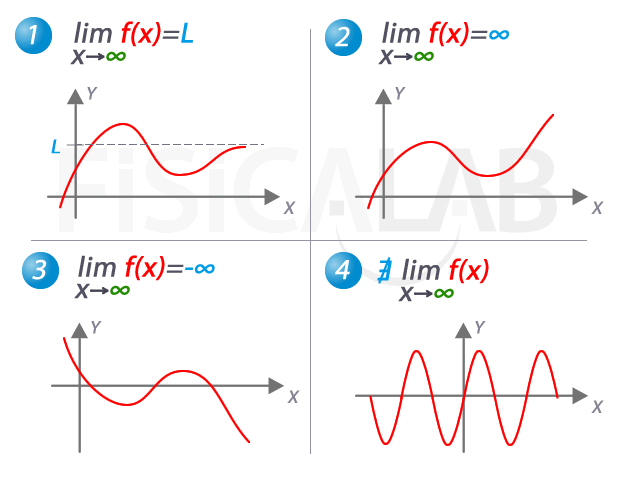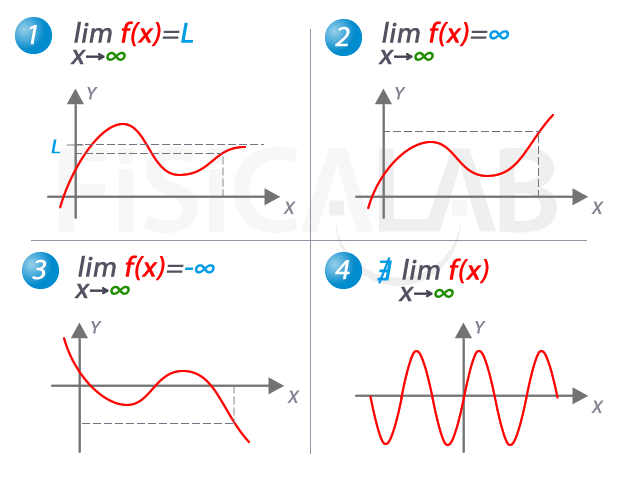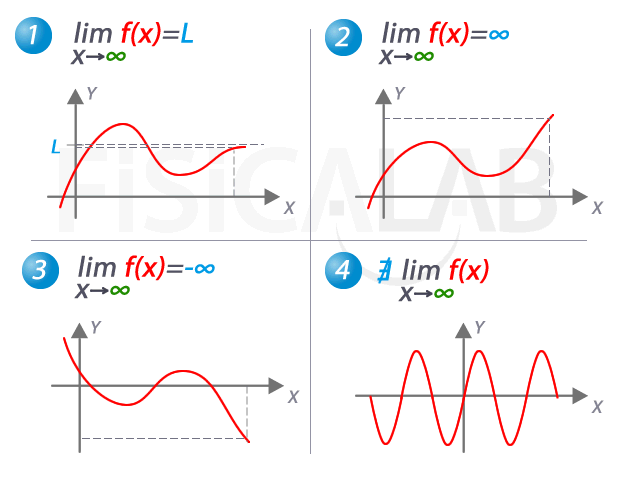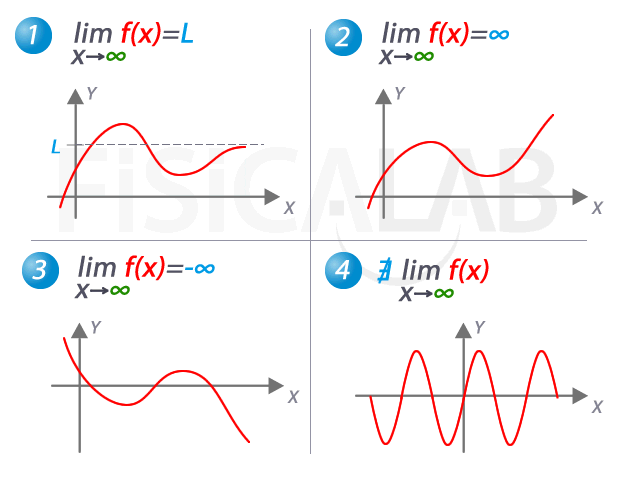
Hasta ahora sólo hemos considerado límites de una función cuando x tiende a un número real a. Sin embargo, también podemos analizar el comportamiento de f(x), cuando x toma valores cada vez más y más grandes, sean estos positivos o negativos; es decir, cuando x → + ∞ (significa que “x” crece sin límite) o cuando x → - ∞ (significa “x” decrece sin límite). Esta clase de límites se denominan límites al infinito

 

 

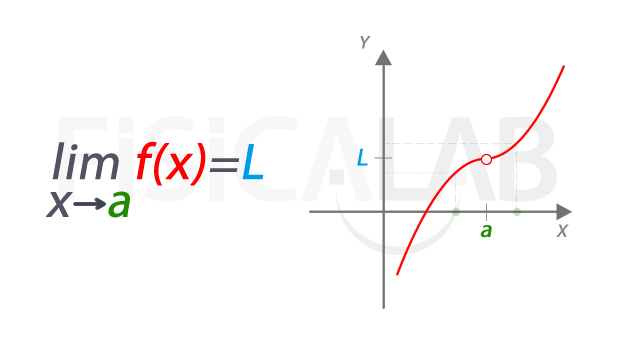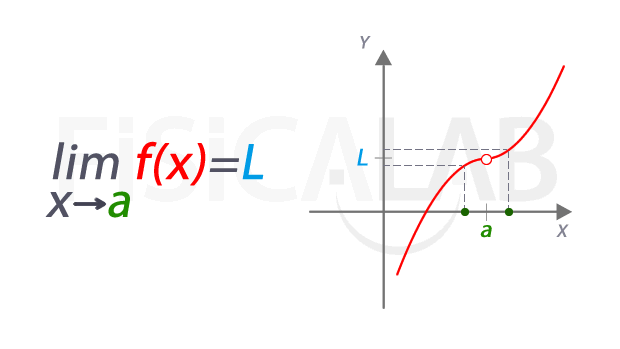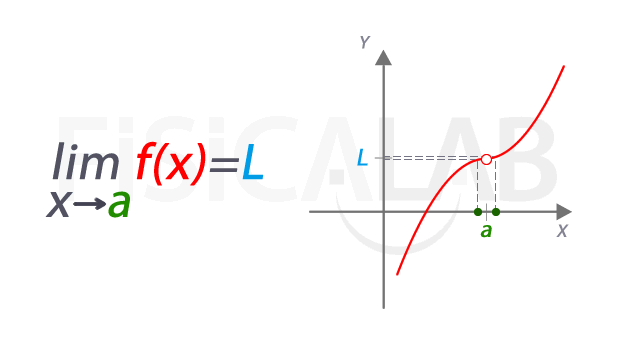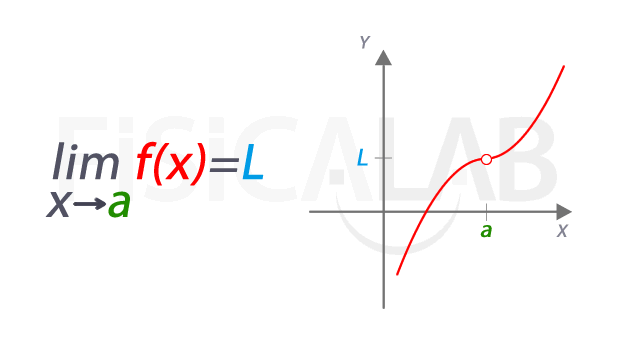
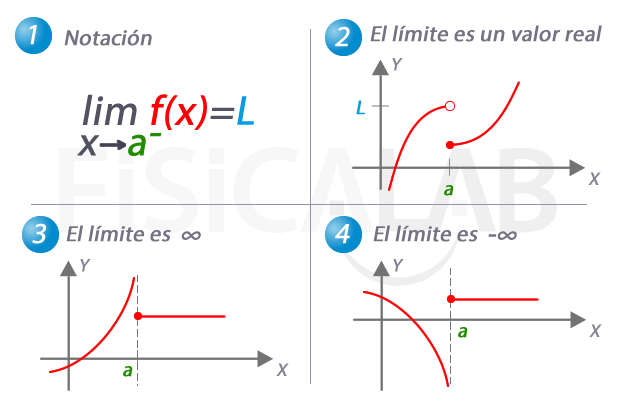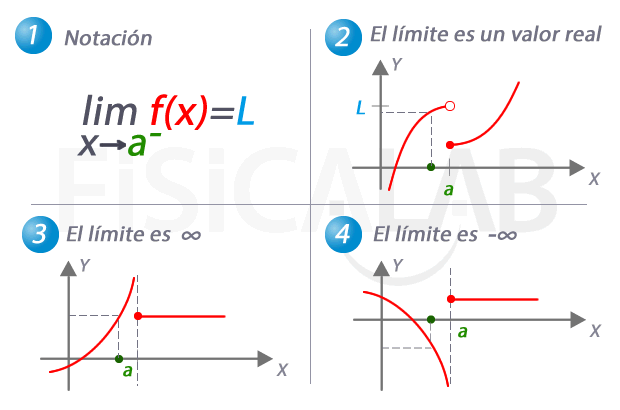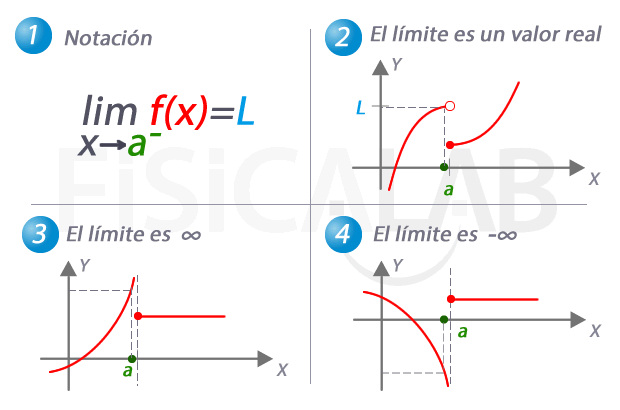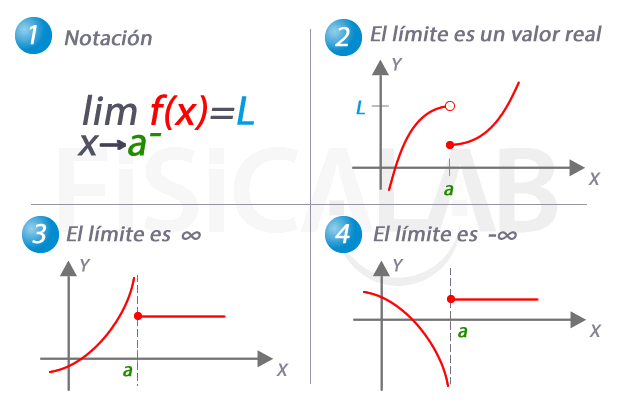
Al evaluar límites al infinito, lo más seguro es que lleguemos a indeterminaciones matemáticas de la forma: ∞ / ∞, ∞ - ∞, 1^∞, 0.∞, ∞⁰. Básicamente, trabajaremos las dos primeras.

Al evaluar el límite, debes tener en cuenta las propiedades de los límites que vimos en la tabla anterior y los siguientes dos TEOREMAS:

Si al evaluar el límite una función racional del tipo f(x) = g(x) / h(x) por sustitución directa obtenemos una indeterminación del tipo ∞ / ∞ , para eliminarla seguimos los siguientes pasos:

1. Comprobar la indeterminación – Aplicamos sustitución directa.
2. Dividimos cada término por la mayor potencia de x 
3. Operamos algebraicamente y simplificando los término semejantes. 
4. Aplicamos las propiedades de los límites.
5. Expresamos simbólicamente el límite.

1.3 Cálculo de un límite

Para determinar el limite de una función analizaremos los siguientes videos

 

 

 

 

 

 

 

 

 

 

 

 

 

Determina los siguientes ejercicios de limites Determinados

 

 

RESPUESTAS

1) 0                                                      10) -995

2) -120                                                 11) 10/19

3) 6                                                       12) 13/8

4) 140                                                   13) 17/4

5) -123                                                  14) 13/20

6) -20                                                    15) 9

7) 257                                                   16) 0

8) 0                                                       17) 0

9) -10                                                    18) 2

 





Limites Indeterminados

factorización de una diferencia de cubos


Limites a infinito

Ejercicios